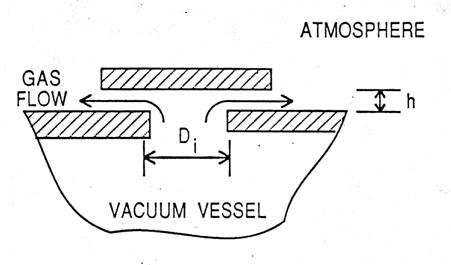
APPENDIX 2b:  RELIEF VENT PRESSURE DROPS

We calculate the pressure drops caused by the flow of gas through tubes and orifices using (CGS units) the following:

Define

G = mass flow (grams/(sec.cm²))

ρ = density (g/cm³)

η = viscosity (poise)

For flow through a tube or channel

         ∆      (1)

where
D_n = effective diameter = 4 x   

         ℓ = length of tube

and

         ψ = 0.326 (GD_n/η) ^-0.25 (turbulent flow)

We also include a “minor loss” term

         ∆P =                        (2)

for the pressure drop occurring at any orifice or sharp bend in the flow channel.  For most relief path geometries term (2) will be larger than term (1).  Application of expression (2) is not always straightforward, a number of examples are discussed in ref. [8].  In what follows we assume the density of helium to scale according to the ideal gas law.

Example I.  Vacuum Vessel Relief Vents

                    These are of the form

We treat this as an orifice with area = the lesser of (πD_ih) or (πD/4) and we take the pressure drop to be given by (2).  We calculate the flow of helium gas through these vents for a pressure drop equal to the cracking pressure P_c plus one PSI.  Under these conditions, the dimensions are:

                  Unit                        P_c                     D_i                     h                      Area

A.          ATLAS Linac          1.1 psi           15.24 cm            2.5 cm              121.6 cm²

B.          Rebuncher               3    psi              5.08                 0.64                    10.2

C           PII^*                         1    psi           15.24                  2.5                   121.6 cm²

^*for PII the overpressure = 2 psi

We assume (conservatively) that

     (ideal gas) at 1 ATM.

For ATLAS:  He at 15.1 K, DP = 2 psi, Vent Area = 121.6 cm²

Using ∆P =    (1 psi = 6.9 x 10⁴ dyne/cm²)

then G = 29.2 g/cm² sec

thus Vent Capacity = 29.9 x 121.6 = 3630 g/s

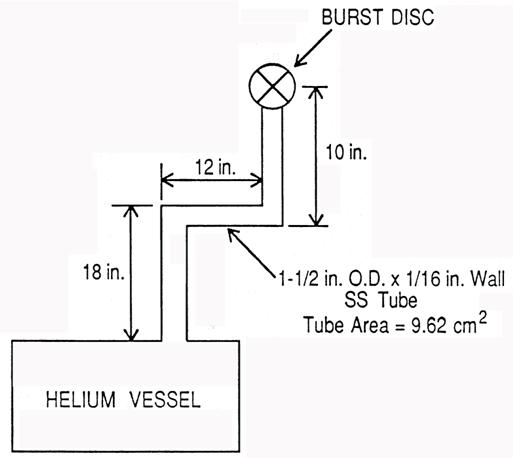
Example II.  Helium Vessel Vent – Rebuncher

 We assume helium gas at 5 K, the dominant term is the “minor loss” term we take

∆P =

at each 90º bend, and at the outlet orifice – working backward from the outlet, and assuming r = 9.8x10^-3 P (g/cc) where P is in atmosphere (ideal gas density), for a total flow of 420 g/sec, G = 420/9.62 = 43.7 g/sec cm²

We note that the frictional loss gives DP₁ = 0.2 psi for this case, and