
This web page presents single-nucleon momentum distributions calculated for a variety of nuclei in the range A=2-12. Corresponding two-nucleon momentum distributions can be found here. These are from variational Monte Carlo calculations (VMC) using either the Argonne v18 two-nucleon and Urbana X three-nucleon potentials (AV18+UX) or one of the Norfolk Δ-full chiral effective field theory interactions: NV2+3-Ia, -Ia*, -Ib*, -IIa*, -IIb*.
Original density and momentum distribution results for AV18+UX were reported
in:
Wiringa, et al., Phys. Rev. C 89, 024305 (2014).
The results with Norfolk chiral EFT interactions are reported in:
Piarulli, et al., Phys. Rev C 107, 014314 (2023).
Please cite the above papers when using results from these pages.
These VMC wave functions are the starting trial functions for a
number of recent Green's function Monte Carlo (GFMC) calculations:
Brida, et al., Phys. Rev. C 84, 024319 (2011);
McCutchan, et al., Phys. Rev. C 86, 024315 (2012);
Pastore, et al., Phys. Rev. C 87, 035503 (2013);
Datar, et al., Phys. Rev. Lett. 111, 062502 (2013);
Pastore, et al., Phys. Rev. C 90, 024321 (2014).
More details of the wave function construction can be found in
Wiringa, Phys. Rev. C 43, 1585 (1991) for A=3,4;
Pudliner, et al., Phys. Rev. C 56, 1720 (1997) for A=6,7;
Wiringa, et al., Phys. Rev. C 62, 014001 (2000) for A=8;
Pieper, et al., Phys. Rev. C 70, 044310 (2002) for A=9,10.
An excellent overall review of quantum Monte Carlo methods for nuclei
can be found at:
The largest nuclei are evaluated using the cluster VMC (CVMC) method.
The CVMC method is described in
The Norfolk interactions are described and used in the following papers:
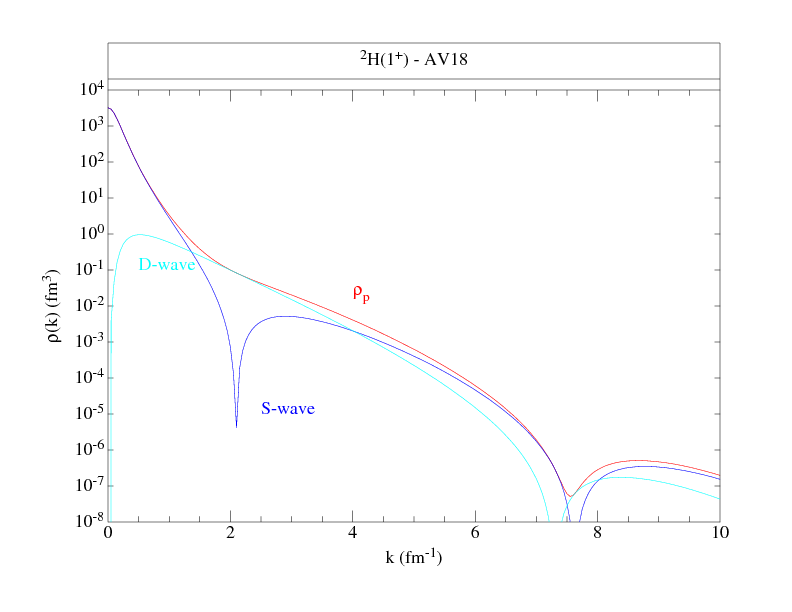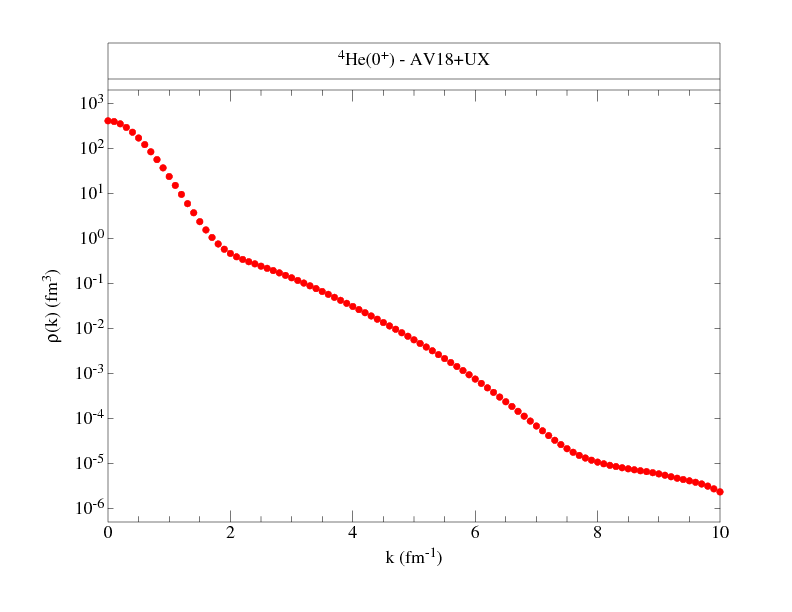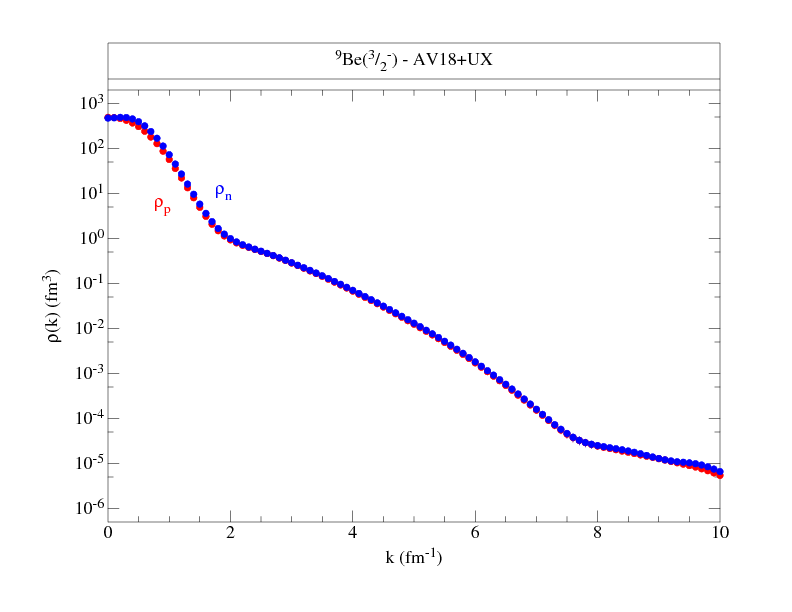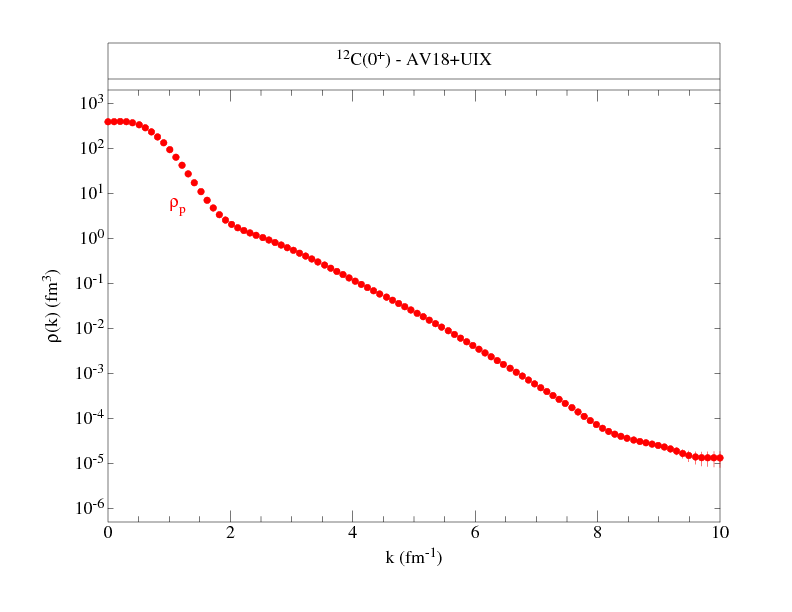
Momentum distributions are provided for neutron spin-down, neutron
spin-up, proton spin-down, and proton spin-up cases, for the M=J state.
The single-nucleon densities corresponding to
these wave functions are given here
Following are files that tabulate the proton and neutron momentum distributions
along with figures to give an overall view of the distributions.
The normalization is chosen such that:
Carlson, et al., Rev. Mod. Phys. 87, 1067 (2015)
Pieper, et al., Phys. Rev. C 46, 1741 (1992) for A=16 with AV1
4+UVII
Lonardoni, et al., Phys. Rev. C 96, 024326 (2017) for A=16,40 with AV18+UIX.
Piarulli, et al., Phys. Rev. C 94, 054007 (2016).
Piarulli, et al., Phys. Rev. Lett. 120, 052503 (2018).
Baroni, et al., Phys. Rev. C 98, 044003 (2018).
Schiavilla, et al., Phys. Rev. C 99, 034005 (2019).
where NS denotes proton or neutron, spin up or down, and ANS is the total number (out of A) nucleons with the given nucleon-spin projection. Where proton and neutron momentum distributions are the same, as in T=0 nuclei, we give only one set, and similarly, if spin-up and spin-down projections are the same, as in 0+ states, we give totals only. The kinetic energy from these distributions is also given.
Robert B. Wiringa
Last updated April 16, 2024